A级毛片免费观看_亚洲国产精品久久久久婷婷老年_欧美日韩国产精品VA_一级黄色视频网页 - 国产91无码福利在线

摘要：GM(1,1)模型是應用范圍極廣的灰指數模型，其精度取決于背景值的構造形式和初始條件的選取。在誤差最小化準則下構建了基于粒子群算法的GM(1,1)模型，同時對模型的背景值系數和初始值進行了優化。運用優化的模型分別對齊次指數序列、2017—2021年我國新能源汽車保有量進行擬合。實例分析表明，基于粒子群算法優化的GM(1,1)模型適合中長期預測并且具有更高的擬合精度。

關鍵詞：GM(1,1)模型；粒子群算法；背景值；初始條件；誤差最小化

中圖分類號：C931    文獻標識碼：B    文章編號：1671-2064(2023)13-0094-05

0 引言

灰色系統理論是由我國著名學者鄧聚龍教授首創的一門系統科學理論，其產生與發展為人們科學認識和解決不確定的系統問題提供了一個新的視角^[1]。GM(1,1)模型作為經典的灰色預測模型，具有所需原始數據量少、計算簡便、適用性強等優點，在農業、工業、經濟管理、工程技術等領域中得到了廣泛應用。然而傳統GM(1,1)模型也存在一定的局限性，當發展系數越大時，GM(1,1)模型的預測精度越低。為提升傳統GM(1,1)模型的精度，擴大適用范圍，學者們進行了大量的研究，結果表明，模型背景值構造以及初始值選取極大程度上影響了預測精度。背景值優化方面，一是優化傳統的背景值公式，如蔣詩泉^[2]利用復化梯形公式優化背景值，王曉佳等^[3]將分段線性插值函數與Newton插值公式相結合，改進了背景值的構造方法。背景值公式優化方法盡管在一定程度上提升了模型精度，但是背景值計算均較為復雜。基于此，張可^[4]結合非線性優化的粒子群算法對背景值參數直接進行尋優，提升了預測精度，擴大了模型使用范圍；楊孝良^[5]提出三參數背景值構造的新方法，提升了背景值的平滑效果；徐寧^[6]基于誤差最小化對GM(1,1)模型背景值進行優化，該方法改善了發展系數較大時建模精度低的不足，保持了較好的無偏性，計算過程也很簡便，但是證明基于原始序列有齊次指數增長規律的前提，限制了模型的適用范圍。初始條件優化方面，熊萍萍^[7]針對非等間距 GM(1,1) 模型的預測問題，提出以非等間距一階累加生成序列各分量的加權平均數作為優化的初始值，通過算例驗證了所提出的非等間距優化模型的有效性和可行性；張彬^[8]將背景值優化公式和邊值修正相結合對模型進行改進；鄭雪平^[9]借鑒徐寧和張彬的思路，將初值優化方法和背景值優化結合起來進行模型優化,使近似齊次指數序列擬合效果得到明顯提升。

為提升模型的適應性，本文利用智能算法實現動態尋優的目的，采用平均相對誤差最小準則，構建適應度函數，將傳統GM(1,1)模型的背景值系數與初始條件同時優化后，運用粒子群算法得到最優值，通過算例對優化后GM(1,1)模型的適用范圍和有效性進行了驗證。

1 傳統GM(1,1)模型

定義1  設原始非負序列，序列

的一階累加序列，，其中，的緊鄰均值生成序列，方程

（1）

稱為GM(1,1)模型的定義式，z⁽¹⁾(k)稱為GM(1,1)模型的背景值，a,b為待定系數。

令 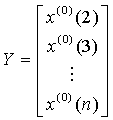 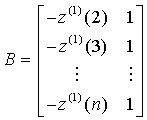，待定系數列[a,b]^T在最小二乘意義下的估計為：

（2）  

定義2 假設X^（0）為非負序列，X^（1）為X^（0）的一階累加序列，a，b，B如定義1中所示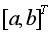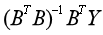， =，稱方程

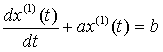（3）

為GM(1,1)模型對應的白化微分方程。

取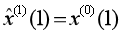為初始條件，將參數a，b代入微分方程求解，可得X^（1）的時間響應式為：

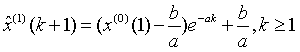（4）

將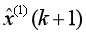序列進行累減，得到原始序列X^（0）的時間響應式為：

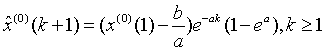（5）

-a，b分別稱為發展系數與灰色作用量,-a反映了預測序列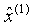和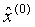的發展態勢。上述建模過程可以看出GM(1,1)模型對原始序列實現預測分成兩個主要步驟：（1）由原始序列生成一階累加序列以及緊鄰均值序列，通過定義式（1）利用最小二乘法估計出參數列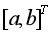；（2）將參數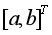列代入白化微分方程，以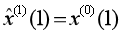為初始條件求出一階累加序列的預測公式（4），一階累減生成原始序列的預測公式（5）。因此，GM(1,1)模型的預測精度取決于：（1）參數列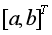的估計精度，顯然，參數列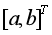通過差分方程傳遞給白化微分方程，為進一步探究定義式與白化微分方程之間的關系，將微分方程（3）兩邊同時從k-1到k積分，得 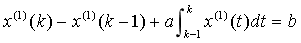，與GM(1,1)模型定義式相比可知，準確的背景值應為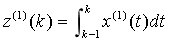，幾何意義為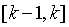區間內曲線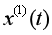到橫坐標軸間的積分面積，而傳統模型中以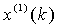和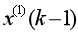的均值取代了準確背景值。由此可知, 背景值構造形式的偏差通過參數列的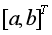估計影響模型擬合誤差精度，形成建模系統的誤差估計精度；（2）灰色微分方程模型初始條件的選取，傳統GM(1,1)模型取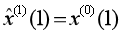作為初始值，這就假定擬合曲線必定過點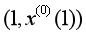，當實際初始值偏離整體規律時，得到的模型也會偏離整體規律，進而影響模型精度，因此初始值的選取至關重要。基于以上分析可知，同時優化背景值和初始條件能夠有效提升模型的預測精度。

2 GM(1,1)模型優化

2.1背景值優化  

定理 1 ，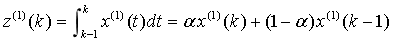

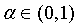
證明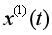：為單調遞增序列，由第二積分中值定理可知，  

，

令

在最小二乘意義下，參數列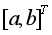的估計值為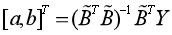：。在傳統GM(1,1)模型中，通常取背景值系數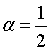。從定積分幾何的意義上來看，傳統模型用梯形面積取代了曲面梯形面積，當累加函數增速較快時，產生的誤差越大，這也是傳統GM(1,1)模型在發展系數-a大于3時擬合誤差逐漸增大主要原因。顯然a的選取與一階累加序列曲線形式密切相關，為提升擬合精度，a的取值應根據序列的性質確定。  

2.2 初始值優化

定理2   相對平均誤差平方和最小準則下，時間響應式常數C最優與初始條件最優等價。

證明： （1）時間響應式常數C最優

2.3 背景值系數a的確定

注意到模型為非線性優化問題，借助非線性無約束優化模型，利用 LINGO、MATLAB 等軟件或者智能算法（粒子群、遺傳算法等）可以實現對背景值系數a的最優化求解。本文采用智能算法中的粒子群優化算法 (PSO)確定最優參數^[10-11]。

3 實例分析

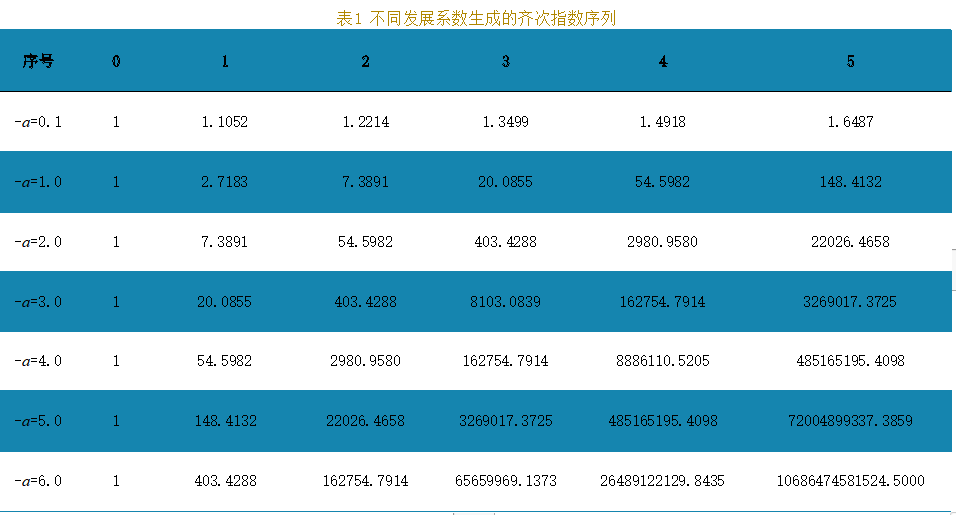
由表2可知，傳統GM(1,1)模型誤差隨著發展系數的增大迅速增加，新的模型精度均高于99%，且隨著發展系數增加，誤差不斷減少，這說明模型能夠高度擬合齊次指數增長序列。

在實際應用方面，選取2017~2021年我國新能源汽車保有量（見表3）為原始序列進行預測，將本文模型的預測結果分別與傳統模型（模型一）、文獻[6]提出的基于誤差最小化的背景值優化GM(1,1)預測模型（模型二）和文獻[9]提出的對初值條件及背景值進行綜合優化的預測模型（模型三）進行對比（見表4）。

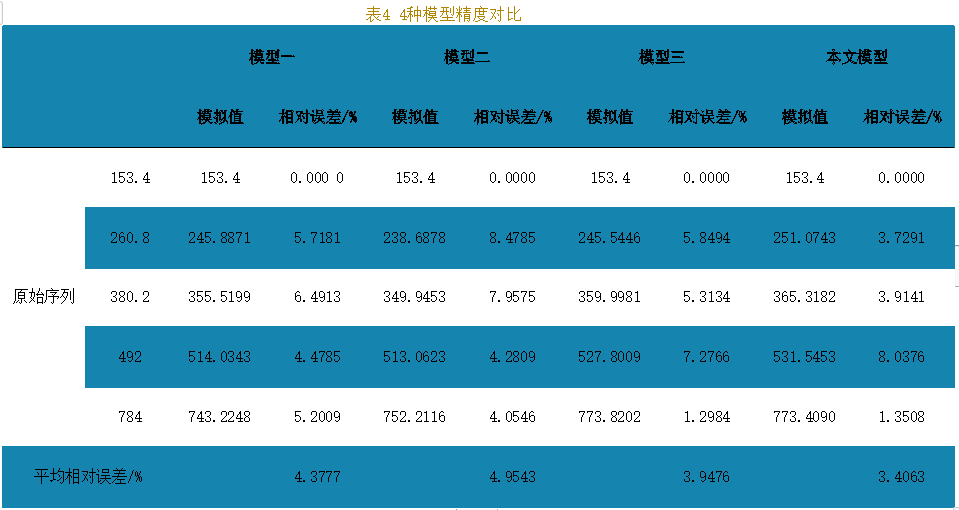
從表4中4種模型的模擬值、相對誤差以及平均相對誤差可知，模型一、模型二、模型三所得模擬數據的平均相對誤差分別為4.3777%、4.9543%、3.9476%，模型的平均相對誤差為 3.4036%，綜合優化模型的預測精度優于其他模型。

4 結語

采用平均相對誤差最小準則，構建適應度函數，結合粒子群算法動態有效尋優的特性，實現了傳統GM(1,1)模型的背景值系數和初始值同時優化。通過對齊次指數序列的模擬分析可知，當發展系數α接近6時，接近完全擬合，這說明提出的模型可用于中長期預測，其適用范圍較傳統GM(1,1)模型有了較大的擴展。實例驗證可知，該模型在預測精度上優于已有的背景值和初始條件綜合優化的GM(1,1)模型。

參考文獻

[1] 劉思峰,黨耀國,方志耕,等.灰色系統理論及其應用[M].北京:科學出版社,2010.

[2] 蔣詩泉,劉思峰,周興才.基于復化梯形公式的GM(1,1)模型背景值的優化[J].控制與決策,2014,29(12):2221-2225.

[3] 王曉佳,楊善林.基于組合插值的模型預測方法的改進與應用[J].中國管理科學,2012,20(2):129-134.

[4] 張可,劉思峰.基于粒子群優化算法的廣義累加灰色模型[J].系統工程與電子技術,2010,7(32):1437-1440.

[5] 楊孝良,周猛,曾波.灰色預測模型背景值構造的新方法[J].統計與決策,2018,(19):14-17.

[6] 徐寧,黨耀國,丁松.基于誤差最小化的GM(1,1)模型背景值優化方法[J].控制與決策,2015,30(2):283-288.

[7] 熊萍萍,黨耀國,姚天祥.基于初始條件優化的一種非等間距 GM(1,1)建模方法[J].控制與決策,2015,30(11):2097-2102.

[8] 張彬,西桂權.基于背景值和邊值修正的GM(1,1)模型優化[J].系統工程理論與實踐,2013,33(3):682-688.

[9] 鄭雪平,王大國,水慶象.基于背景值和初始條件綜合優化的GM(1,1)預測模型[J].統計與決策,2021,(9):25-28.

[10] 王亮,滕克難,呂衛民,等.基于粒子群算法的非線性時變參數離散灰色預測模型[J].統計與決策,2015,(12):16-19.

[11] 于麗亞,王豐效.基于粒子群算法的非等距GOM(1,1)模型[J].純粹數學與應用數學,2011,27(4):472-475.

Optimization of GM(1,1) Model Based on Particle Swarm Algorithm

WANG Luxin

(Basic teaching department, Jiangsu Shipping College, Nantong  Jiangsu  226010)

Abstract:GM (1, 1) model is a gray index model with a wide range of applications, and its accuracy depends on the structure of the background value and the selection of initial conditions. The article proposes a GM (1, 1) model based on the particle swarm algorithm to optimize the background value coefficients and initial conditions under the error minimization criterion. The optimized model is used to fit the sub-index sequence, the number of new energy cars of China from 2017 to 2021 , and the wind power generation of China from 2012 to 2020. The example analysis shows that the new optimized GM (1, 1) model is suitable for medium and long-term prediction and also has higher accuracy.

Key words:GM(1,1) model;particle swarm optimization;background value;initial condition;error minimization